Serie: About Early Math
Más allá de Base-10: sistemas inusuales para contar

Contar es una de las primeras habilidades matemáticas que desarrollan las niñas y niños. Aunque contar hasta diez es un hito importante, también es un obstáculo temporal porque se quedan sin dedos para contar. A partir de ahí, vemos que cada décadao serie de diez, es un mini-hito que las niñas y niños deben conquistar. Observe cómo este niño hace una pausa y añade énfasis cada vez que cruza a una nueva década.
Está claro que contar en juegos de diez, también llamado base-10 o sistema numérico decimales una habilidad que desarrollamos e interiorizamos a una edad muy temprana. Sin embargo, sorprendentemente, existen docenas de sistemas de conteo diferentes, muchos de los cuales siguen utilizándose en la actualidad. Entender y explorar otros sistemas de conteo puede ser útil para los niños más adelante, cuando intenten medir un objeto que no sume limpiamente 10 unidades. También es útil cuando los niños empiezan a abordar "la temida palabra F". fracciones.
-
El sistema de conteo de Shepherd
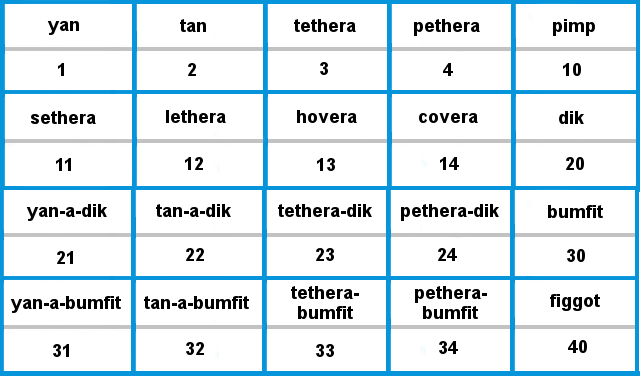
Los alumnos de más edad pueden disfrutar tratando de entender este sistema de conteo. Hace años, los pastores de Escocia, Inglaterra y Gales contaban sus ovejas siguiendo este conjunto de reglas, y algunas de estas palabras para contar siguen apareciendo coloquialmente en las regiones rurales. Hay variaciones regionales, pero la mayoría se ocupa exclusivamente de los números hasta el 20. A menudo tienen una sub-base de 5 entre 10 y 20, por lo que puede ser una vía para explorar una sistema base-5. sistema. Escrito en los números arábigos que conocemos, un ejemplo del sistema de conteo de un pastor podría verse y sonar así:
Este gráfico parece que llega hasta 40pero 20 es la cantidad real alcanzada. Vemos el número 40 escrito, porque al utilizar el valor posicional en un sistema de base 5, llegaríamos a una nueva década después de cada quinto número.
Este ejemplo es divertido, pero a no ser que tenga previsto viajar a la Escocia rural, es posible que no tenga la oportunidad de utilizarlo muy a menudo. En un aula de educación infantil, profundizar en este sistema numérico diferente, quizá incluso con un poco de historia europea y un giro cultural en la lección, puede ser una exploración útil.
-
Binario (base-dos)
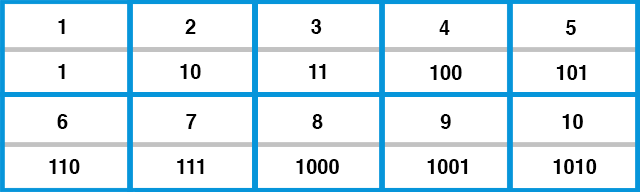
Existe un sistema numérico no decimal que seguramente utilizas a diario y que estás utilizando ahora mismo al leer este artículo. Los ordenadores y la electrónica utilizan este sistema numérico para realizar la mayor parte de su procesamiento. Tal y como suena, sólo utiliza dos dígitos diferentes, el 0 y el 1. Su aspecto es el siguiente:
El año 2014 quedaría así: 11111011110. Es bastante difícil de leer. ¿Por qué los ordenadores utilizan sólo dos dígitos? Piensa en otro aparato eléctrico que utilizas a diario: un interruptor de la luz. Tienes dos opciones: pulsarlo hacia arriba para encenderlo y pulsarlo hacia abajo para apagarlo. Es muy fácil determinar si las luces están encendidas o apagadas; ¡o estás sentado en la oscuridad o no lo estás! Esta lógica de "encendido o apagado" es exactamente la que utilizan los ordenadores y, por tanto, la razón por la que nos encontramos con el binario todos los días, nos demos cuenta o no. Ayuda a los ordenadores a procesar y almacenar números, letras y funciones más complejas de forma rápida y eficaz.
-
Doceal (base-doce)
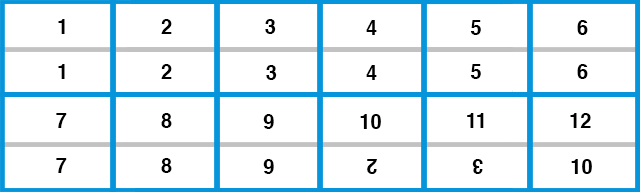
Este sistema de recuento no se utiliza de forma generalizada en ningún sitio, pero The Dozenal Society of America presenta una serie de argumentos matemáticamente convincentes sobre por qué debería serlo, especialmente en comparación con el sistema de base 10 al que estamos tan intrínsecamente ligados. Es así:
Hay que tener en cuenta que para tener una década completa, hay que añadir dos números. Estos se escriben comúnmente como un 2 y un 3 invertidos, llamados dek y el, y representan las mismas cantidades que 10 y 11.
La simplificación de los conceptos matemáticos básicos es una de las razones principales de su argumento. Tal vez el más convincente sea su argumento sobre las fracciones, un concepto temido por muchos alumnos jóvenes que podría hacerse mucho más fácil implementando un sistema de docenas. ¿Cómo? Las fracciones más comunes que utilizamos -conocidos como tercios y cuartos- se representan fácilmente con este sistema, porque el 12 es divisible por igual entre 2, 3 y 4 (además de, por supuesto, el 6). El diez, en cambio, sólo puede dividirse limpiamente en mitades y quintas. Por eso, enseñar a los alumnos algo tan sencillo como la división equitativa de una pizza entre tres amigos (1 ÷ 3 = 0,3) introduce ideas potencialmente confusas o que distraen sobre el infinito a través de los decimales recurrentes.
Pero, ¿qué pasa con los dedos en los que los niños confían para contar tan pronto? Lo ideal es que no dependan del conteo con los dedos durante mucho tiempo en su carrera matemática. Sin embargo, si les sirve de ayuda, pueden utilizar las articulaciones del interior de sus cuatro dedos como herramientas para contar (véase la imagen al principio de este artículo).
¿Le parecen estas ideas descabelladas? Piensa en lo siguiente: cuando dices la hora, utilizas simultáneamente versiones simplificadas de base-12 y base-60 (piensa en lo que ocurre el minuto después de las 12:59). Al medir telas, utilizas la idea de los sistemas de conteo de base-12 y base-3 (2 yardas, 1 pie y 3 pulgadas). ¿Estás haciendo un pastel? Probablemente necesitarás una hoja de trucos para asegurarte de que estás midiendo correctamente. Pensar en estos sistemas de recuento poco habituales puede ser un divertido ejercicio mental para los alumnos. También puede ayudarles a ver los números y los métodos que utilizan a diario bajo una nueva luz.