Series: About Early Math
Beyond Base-10: Three Unusual Counting Systems

Counting is one of the first mathematical skills that children develop. While counting to ten is a major milestone, it is also a temporary roadblock because children run out of fingers to count on! From there, we see that each decade, or series of ten, is a mini-milestone for young students to conquer. Note how this student pauses and adds emphasis every time he crosses into a new decade.
It is clear that counting in sets of ten, also called a base-10 or decimal numeral system, is a skill that we develop and internalize at a very young age. However, surprisingly, there are dozens of different counting systems, many still in use today. Understanding and exploring other counting systems can be helpful to children further down the line when attempting to measure an object that does not cleanly add up to 10 units. It is also helpful when children begin to tackle “the dreaded F word,” fractions.
-
Shepherd’s Counting System
Older students might enjoy trying to wrap their heads around this counting system. Years ago, shepherds in Scotland, England, and Wales counted their sheep using this set of rules, and some of these counting words still pop up colloquially in rural regions. There are regional variations, but most deal exclusively with numbers up to 20. They often have a sub-base of 5 between 10 and 20, so it may be an avenue for exploring a base-5 system. Written in the Arabic numerals that we know, an example of a Shepherd’s counting system might look and sound like this:
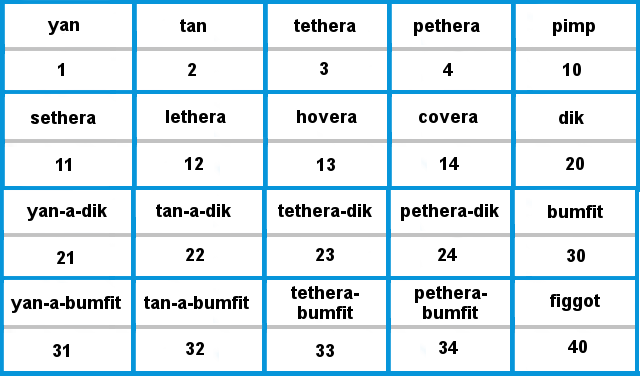
This chart looks like it goes up to 40, but 20 is the actual quantity reached. We see the numeral 40 written, because when using place value in a base-5 system, we would reach a new decade after every fifth number.
This example is fun, but unless you plan on traveling to rural Scotland, you might not get the chance to use it very often. In an early education classroom, delving into this different number system, maybe even with a little European history and cultural spin to the lesson, can be a useful exploration.
-
Binary (base-two)
There is a non-decimal number system you most likely use every day and are actually using right now reading this article. Computers and electronics use this number system to do the bulk of their processing. As it sounds, it uses only two different digits, 0 and 1. It looks like this:
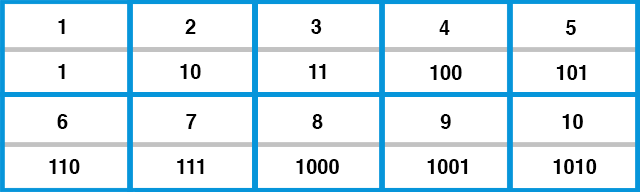
The year 2014 would look like this: 11111011110. It’s pretty hard to read. Why would computers use only two digits? Think of another electric device you use daily: a light switch. You have two choices: flip it up to turn it on; flip it down to turn it off. It’s very easy to determine whether the lights are on or off; you’re either sitting in the dark or you aren’t! This “on or off” logic is exactly the logic that computers use and is therefore the reason we encounter binary every day, whether we realize it or not. It helps computers process and store numbers, letters, and more complex functions quickly and efficiently.
-
Dozenal (base-twelve)
This counting system isn’t widely in use anywhere, but The Dozenal Society of America makes a number of mathematically convincing arguments about why it might ought to be, especially in comparison to the base-10 system that we are so intrinsically tied to. It looks like this:
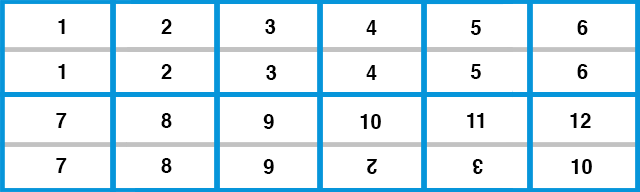
Note that in order to have a full decade, we need to add two numerals. These are commonly written as an upside down 2 and 3, called dek and el, and represent the same quantities as 10 and 11.
Simplifying fundamental early math concepts is actually a leading reason in their argument. Perhaps most convincing is their argument about fractions, a concept dreaded by many young learners that could conceivably be made much easier by implementing a dozenal system. How? The most common fractions we use—halves, thirds, and quarters—are easily represented using this system, because 12 is evenly divisible by 2, 3 and 4 (as well as, of course, 6). Ten, on the other hand, can only be split cleanly into halves and fifths. Because of this, teaching students something as simple as how to split a pizza fairly among three friends (1 ÷ 3 = .3) introduces potentially confusing or distracting ideas about infinity through recurring decimals.
But what about the fingers that children rely on to count so early on? Ideally they won’t rely on finger-counting too long into their math careers. However, if it helps, they can use the joints on the insides of their four fingers as counting tools (see the image at the beginning of this article).
Do these ideas seem outlandish to you? Consider this: when telling time, you simultaneously use simplified versions of base-12 and base-60 (think about what happens the minute after 12:59). When measuring fabric you are making use of the idea of base-12 and base-3 counting systems (2 yards, 1 foot, and 3 inches). Baking a cake? You’ll probably need a cheat sheet to make sure you’re measuring correctly! Thinking about these unusual counting systems can be a fun mind-teaser for students. It can also help them see the numbers and methods that they use every day in a new light.